Séminaire SFR MathSTIC - Calcul de la topologie de variétés,algébriques de petite dimension14h00 | Faculté des sciences | amphithéâtre D - bâtiment A | 2, boulevard Lavoisier | ANGERS

Le 22 septembre 2022

Programme

14h00-14h30 : Une (très) courte introduction à la géométrie algébrique réelle. Nicolas Delanoue, LARIS - Université d'Angers.

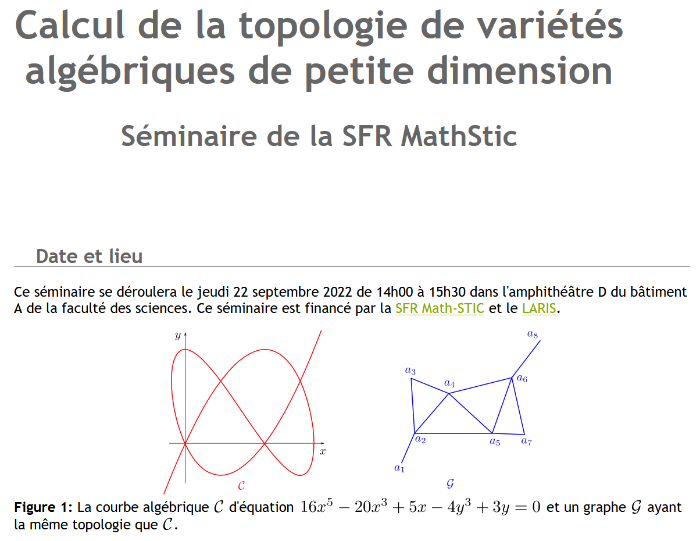
L'exposé commencera par motiver l'étude de ces sous-ensembles de avec des problèmes issus de la robotique : planification de trajectoires, étude de singularités, mode d'assemblage.
Dans un second temps, on exposera plusieurs techniques algorithmiques classiques comme la méthode de Sturm ou encore la théorie des résultants. La première permet de dénombrer (et isoler) algorithmiquement les racines réelles d'un polynome d'une variable. Avec la théorie des résultants, il est possible de décider que deux polynômes ont une racine en commun. Employées correctement, ces deux méthodes permettent de calculer la topologie d'un ensemble semi-algébrique de . Lors de cette présentation, de nombreux exemples seront donnés en dimension 2.
Finalement, la complexité en temps de ces algorithmes sera discutée en tenant compte de la taille potentielle des mots mémoires mis en jeu lors de l'exécution. Les exposés suivants proposeront des algorithmes calculant la topologie de courbes algébriques du plan ayant de meilleures complexités. Résumé complet

14h30-15h00 : Comment dessiner une courbe correctement ? Marc Pouget, GAMBLE, INRIA Nancy, LORIA lab.

Résumé : Tout logiciel de calcul permet de visualiser une courbe définit implicitement par une équation. Cependant, rares sont les logiciels apportant des garanties sur la topologie du résultat. Dans le cas d'une courbe algébrique, nous rappellerons les difficultés de l'algorithme classique de décomposition cylindrique algébrique et proposerons une alternative utilisant des représentations univariées rationnelles (RUR). En particulier, nous présenterons les idées permettant d'obtenir la meilleure complexité de l'état de l'art pour calculer les RURs avec un algorithme de type Las Vegas (l'algorithme est probabiliste avec un résultat garanti dont on étudie la complexité en moyenne). Un serveur de calcul de topologie et visualisation de courbes est disponible sur https://isotop.gamble.loria.fr
Résumé complet

15h00-15h30 : Calcul efficace de la topologie d'une courbe algébrique plane définie comme l'ensemble des zéros d'un polynôme bivarié de degré d. Daouda Diatta, Université Assane SECK de Ziguinchor. Sénégal.

Résumé : Il est bien connu que le comptage et la localisation des racines réelles d'un polynôme univarié réel est la pierre angulaire de la plupart des algorithmes calculant la topologie des courbes algébriques réelles planes. En effet isoler les racines réelles du discriminant de la courbe algébrique (correspondant à la projection des points singuliers et critiques de la courbe sur l'axe des abscisses) et déterminer les fibres de la courbe en ces racines du discriminant sont des étapes incontournables pour toutes les méthodes basées sur l'approche Décomposition Cylindrique Algébrique.
Nous présenterons un algorithme récent qui calcule, sans conditions de généricité ni changement de variable, la topologie d'une courbe algébrique plane définie comme l'ensemble des zéros d'un polynôme bivarié de degré d et de coefficients entiers de taille binaire bornée par \tau en O(d^5*\tau+d^6) opérations binaires. Résumé complet

Crédits pour les doctorants

Des certificats de participation seront délivrés à tous les doctorants qui en feront la demande, afin qu'ils puissent potentiellement s'en prévaloir auprès de leur école doctorale.