Projet de Recherche APACOSI

Apprentissage Profond et Connaissances Structurelles pour l'analyse d'Images

Équipe :  Information, Signal, Image et Sciences du Vivant

Labellisation : aucune

Durée : 36 mois (01/09/2019 - 01/09/2022)

Financement : RFI Atlanstic 2020, Université d'Angers

Personnels impliqués du LARIS : Jean-Baptiste Fasquel, Jérémy Chopin (doctorant)

Partenaires du projet : Harold Mouchère (LS2N/IPI), Rozenn Dahyot (Trinity College Dublin, Irelande), Isabelle Bloch (LTCI, Paris)

Résumé et objectifs

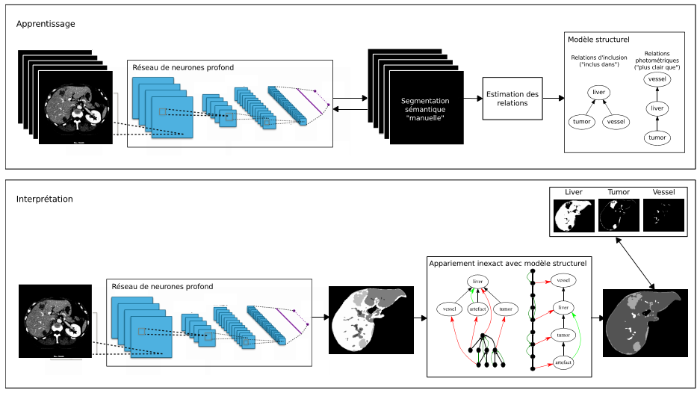
Les récentes recherches en analyse d’images montrent le potentiel de techniques d’apprentissage fortement supervisées telles que l’apprentissage profond. Les principales limites de ce type d’approche sont la nécessité d’une base d’apprentissage conséquente, souvent difficile à acquérir, et la difficulté d’entraîner le modèle comprenant plusieurs milliers de paramètres, même si des techniques de transfert permettent d’accélérer cet apprentissage. Avant cette révolution, les approches ad-hoc nécessitaient beaucoup moins de données mais beaucoup d'expertise pour choisir les bonnes informations à utiliser et les bons outils pour les combiner. Les approches d'analyse structurelle en sont un bon exemple : l'image est découpée en petites entités (composantes connexes, super-pixels, régions, objets...) avec des relations (spatiales, photométriques...) qui constituent un graphe permettant l'analyse structurelle de l'image.

Une telle analyse ad-hoc est souvent coûteuse (e.g. appariement de grands graphes). Le défi que nous proposons de relever dans ce projet est de tirer parti des deux approches : un apprentissage profond avec moins de données d'apprentissage grâce à l’utilisation de connaissances structurelles a priori, pour finalement produire un résultat structuré. L’approche proposée est de s’appuyer sur une connaissance a priori qualitative structurelle (relations spatiales, photométriques...), plus simple à définir et à formuler (e.g. « à droite de », « inclus dans », « plus sombre que »).  Ce type d’approche faiblement supervisée imite le système visuel humain pour appréhender le contenu d’une scène, en travaillant sur les relations qualitatives observées. On souhaite également s’intéresser à l’interprétation séquentielle de la scène, à la manière dont fonctionne la vision humaine, où les structures les plus saillantes sont tout d’abord identifiées. On s’appuie alors sur les relations a priori connues ainsi que sur les structures déjà identifiées pour extraire et identifier les suivantes, selon une stratégie à définir [1] [2]. Ce type d’approche séquentielle est souvent employée dans le cas de scènes complexes pour lesquelles un traitement global n’est pas adapté.

Les verrous à lever sont :

- Comment coupler ce type d’approche structurelle à des approches fortement supervisées de type « apprentissage profond », tout en réduisant la taille de la base d’apprentissage ?

- Comment, dans le cas d’un traitement séquentiel, apprendre la meilleure stratégie d’analyse ?

Concernant le premier verrou, l’objectif est de trouver comment intégrer les connaissances structurelles aux réseaux de neurones (e.g. apprentissage profond). Une première piste consistera à dédier l'extraction des entités de base à un réseau convolutionnel profond [3], à évaluer si les relations entre les entités produites correspondent aux relations a priori, par exemple en s’appuyant sur de l’appariement de graphes [1] [4]. On étudiera le bénéfice de cette approche, notamment sa capacité à réduire le volume des données requis pour l’apprentissage.

Concernant le second verrou, la stratégie consistera à étudier le couplage des informations de structure avec l’usage de techniques telles que l’apprentissage par renforcement ou les modèles récurrents à attention  [5] [6]. Ce type de technique, basée sur la notion de récompense à maximiser, permettra de déterminer la meilleure séquence d’analyse [2]. Cette récompense pourra être évaluée en concevant une métrique permettant de quantifier l’adéquation entre le résultat obtenu et les informations structurelles a priori, par exemple en définissant des distances entre relations (a priori et obtenues) et prenant en compte leur qualité  [7].

Ces travaux seront évalués sur des bases de données adaptées à l’usage d’une information structurelle, en privilégiant les applications médicales (relations entre les structures anatomiques et pathologiques), domaines d’applications au cœur des compétences des partenaires du projet.

Bibliographie

[1] J.-B. Fasquel et N. Delanoue, «An approach for sequential image interpretation using a priori binary perceptual topological and photometric knowledge and k-means based segmentation», Journal of the Optical Society of America A, 2018.

[2] G. Fouquier, J. Atif et I. Bloch, «Sequential model-based segmentation and recognition of image structures driven by visual features and   spatial relations», Comp. Vision & Image Understanding, 2012.

[3] G. Roman-Jimenez, C. Viard-Gaudin, A. Granet et H. Mouchère, «Transfer Learning for Structures Spotting in Unlabeled Handwritten Documents  using Randomly Generated Documents», International Conference on Pattern Recognition Applications and Methods, 2018.                   

[4] J.-B. Fasquel et N. Delanoue, «A graph based image interpretation method using a priori qualitative inclusion and photometric relationships», IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018.                     

[5] V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, S. Petersen, C. Beattie, A. Sadik, I. Antonoglou, H. King, D. Kumaran, D. Wierstra, S. Legg et D. Hassabis, «Human-level control through deep reinforcement learning», Nature, vol. 2015.                

[6] V. Mnih, N.  Heess et A. Graves, «Recurrent models of visual attention», In Advances in neural information processing systems, 2014.                

[7] I. Bloch et J. Atif, «Defining and computing Hausdorff distances between distributions on the real line and on the circle: link between optimal transport and morphological dilations», Mathematical Morphology: Theory and Applications, 2016.